[DS] Affine 변환

1. 선형 변환

선형성 linearity

• 수학에서 선형성은 두 가지로 정의된다.
  • Additivity : $f(a + b) = f(a) + f(b)$
  • Homogeneity : $f(c a) = f(a)$ ($c$는 상수)
• 기억하기 위해서 $f(c_1a + c_2b) = c_1f(a) + c_2f(b)$를 만족하면 선형의 두 조건을 만족하는 셈이다. 앞으로 이 식으로 선형성을 확인하겠다.

선형 함수 linear function

단일 변수 일차 함수

• “선형”이라는 말 때문에 선형 함수를 1차 함수로 오해할 수 있다.
• 일반적인 단일 변수 일차 함수는 $f(x) = m x + n$로 표현할 수 있다.

[ f(c_1a + c_2b) = m(c_1a + c_2b) + n = mc_1a +mc_2b +n \cdots (1)
c_1f(a) +c_2f(b) = mc_1a +mc_2b + 2n \cdots (2)]

• (1)과 (2)가 다르기 때문에 일반적인 일차 함수는 선형함수가 아니다.
• 일차 함수 중 y절편이 0인 경우에만 선형 함수다.

다변수 일차 함수

• 다변수 일차 함수는 $f(\vec{x}) = f(x_1,x_2, \dots,x_n) = m_1 x_1 +m_2x_2 +\cdots + m_nx_n + n$로 표현할 수 있는데 마찬가지로 이 중 $n$이 0인 경우에만 선형 함수라고 할 수 있다.
• 아래의 $f$는 선형이 아니지만, $g$는 선형이다.

[f(x_1, x_2) = 2x_1 + 3x_2 +1 ,\,\, \,\,g(x_1, x_2) = 2x_1 +3x_2 ]

선형 변환 linear transformation

• $\vec{y} = f( \vec{x})$ 처럼 독립 변수 뿐만 아니라 종속변수도 vector인 경우도 가능하다. 이 경우에 독립 변수에 대해 1차 함수라면 벡터와 행렬의 곱셈으로 표현할 수 있다.
• 앞서 설명한 선형성 판정과 비슷한 방식으로 $\vec{y} = \mathbf{A}\vec{x}$는 선형변환이지만 $\vec{y} = \mathbf{A}\vec{x} +\vec{b}$는 선형변환이 아니다.

2. Affine 변환

• Affine 변환은 점은 점으로, 선은 선으로, 면은 면으로 유지하는 변환인데, $\vec{y} = \mathbf{A}\vec{x} +\vec{b}$ 처럼 선형 변환 + 평행 이동이라고 생각하면 된다.
• 위의 식에서 $\vec{b}$를 더하는 과정을 행렬과 벡터의 곱 계산 안으로 넣을 수 있다.
• A 행렬의 마지막 열에 $\vec{b}$를 포함시키고, $\vec{x}$의 마지막 요소에 1을 추가해 다음과 같이 만들면 $\vec{y} = \mathbf{A}\vec{x} +\vec{b} = \mathbf{A’}\vec{x’}$ 로 만들 수 있다.

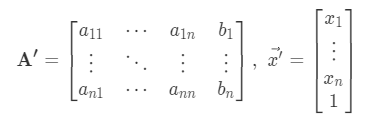
• 이러한 방식으로 Affine 변환도 행렬과 벡터의 곱으로 표현할 수 있다.

Neural Network

• Neural network의 layer는 입력 feature들의 linear transformation에 bias를 더하는 affine transformation 후 activation function에 통과시켜 비선형 변환을 하는 역할을 한다.
• 이 과정은 다음과 같은 수식으로 표현되고, 이를 도식화하면 그 아래의 그림과 같이 표현할 수 있다. $\mathbf{W}$는 weight matrix이고, $\vec{b}$는 bias이다.

[ \vec{y} = \mathbf{W}\vec{x} + \vec{b} \cdots \mathsf{Affine\, Transformation}\{}\ \vec{\sigma} = \mathbf{activation_function}(\vec{y}) \cdots \mathsf{non -linear \, transformation}]

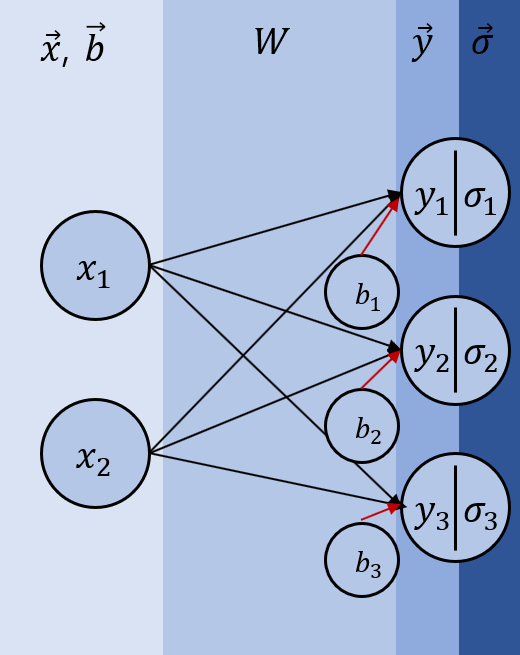
• 위의 식을 앞에서 했던 방식처럼 하나의 matrix와 vector의 곱으로 바꿔 $\vec{y} = \mathbf{W’}\vec{x’}$표현하면 bias가 weight matrix 안으로 들어가는 셈이 되고, 그래프는 다음과 같이 다시 그릴 수 있다.

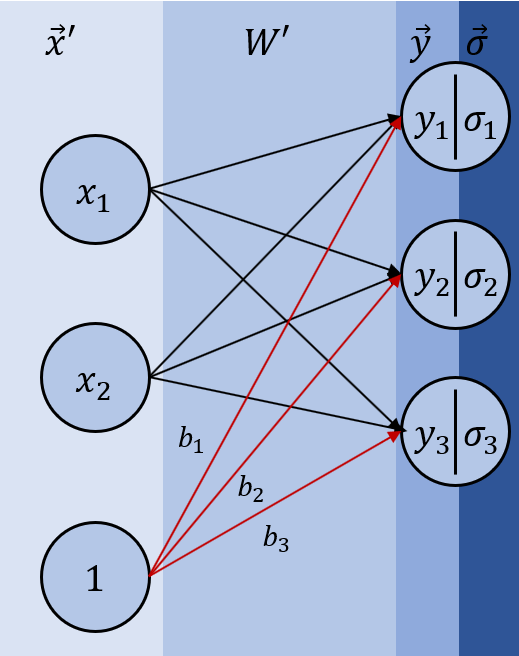
Affine transformation의 다른 의미는 2를 참고

마무리

• 처음 공부할 때 Linear transformation과 Affine transformation 모두 행렬의 곱으로 표현해 혼란스러웠던 기억이 있어 지금까지 공부하며 이해한 내용을 정리를 해봤다.

Reference

[1] wiki - linearity
[2] youtube - 홍정모님 Affine transformation
[3] coursera - Andrew Ng 교수님의 Machine Learning 강의